中学受験の文章問題で必ず出題される問題の一つに、『つるかめ算』があります。しかし、『つるかめ算』は公立の小学校では習いません。その理由としては、学習指導要領に載っていないからだそうです。
しかし中学受験指導の進学塾や、私立小学校及び私立大学付属小学校の一部、国立大学付属小学校の一部 など、独自のカリキュラムを有している小学校では授業の中で教えることもあります。
さらにカリキュラムには無いけれども、先生が独自で授業に教えることはあるかもしれません。とは言え、中学受験ではかなりの高確率で出題される問題です。
===
以前、子どもの宿題に「つるかめ算」のプリントが出たことがあり、親子で四苦八苦しながら解いたことがります。そこで今回は、誰でも簡単に分かる「つるかめ算」の基本的な解法を紹介します。
つるかめ算の基本的な問題と2つの解き方
まずはつるかめ算の基本的な問題から、2つの解き方を確認してみましょう。
■基本問題
つるとかめが合わせて10匹います。足の数の合計は28本です。鶴と亀はそれぞれ何匹ずついるでしょうか?
1.表を使って解く方法
まずは順番に当てはめて解くという、最も基本的なパターンの考え方です。
ここで、まずポイントになるのが、「全部つるだった場合」もしくは、「全部かめだった場合」の足の数を考えます。今回は「全部がかめだった場合」で考えてみましょう。
■10匹全部がかめだった場合の式
10匹×4(かめの足の数)=40本
足の数の合計が40本なので、全てがかめではないことが分かります。次にかめを1匹減らして「かめが9匹、つるを1羽」で考えてみましょう。
■かめ19匹、つる1羽だった場合の式
19匹×4(かめの足の数)+1羽×2(つるの足の数)=38本
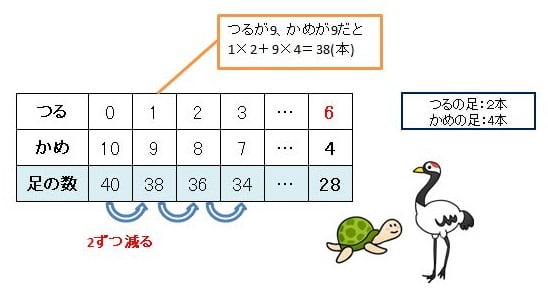
このように、かめの数を1匹減らしてつるの数を1羽増やしていくと、足の数は2ずつ減ることが分かるはずです。これを足の数が28になるまで繰り返すと答えが求められます。
表に表して考えると分かりやすいですよね。しかし、数が大きくなると表にするのは大変です。そこで、もっと早く計算する方法としてつる、またはかめの余った脚の本数を、足の本数の差で割ればもう片方が何匹か計算できます。
■かめの足からつるの数を求める場合
(40-28)÷2=6
10-6=4
答え:つる6羽、かめ4匹
■つるの足からかめの数を求める場合
(28-20)÷2=4
10-4=6
答え:つる6羽、かめ4匹
2.図形を使っての解き方
同じ問題でも図形を使って考えることもできます。
つるかめ算を図形で考える場合は、上のように左右2つの長方形を組み合わせた図形を使います。
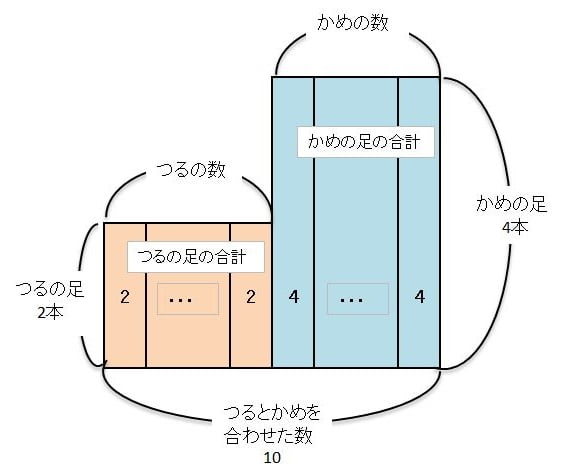
片方は「つるの足の合計を表す長方形」、もう片方が「かめの足の合計を表す長方形」です。横の長さで頭の数を表し、たての長さで1匹(1羽)あたりの足の数を表しています。
まずは、表と同じで全部が「かめだったら」「つるだったら」を考えてみましょう。今回は「全部かめだったら」を基準に考えてみます。
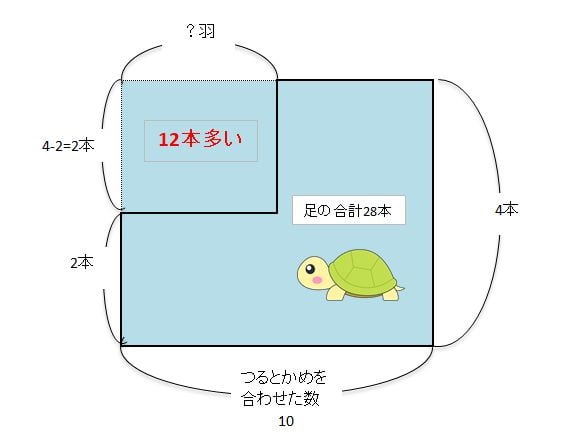
上の図のように全部がかめだとすると、足の合計は40本になるはずです。しかし実際の足の数は28本なので12本多い計算になります。
そこで、かめ1匹をつる1羽に変えていくと、足の数を2本ずつ減らすことができます。12本の足の数を減らせばよいということは、余分な足の数(12)を、つるとかめの足の差(2)で割り算をして、「12÷2=6」になるのです。これを式で表すと次のようになります。
■式に表したとき
1.全部かめだったとすると、足の総数は:4×10=40本
2.本当の足の数との差は:40-28=12本
3.面積図よりつるの数は:12÷2=6羽
4.全部で10匹なのでかめの数は:10-6=4匹
答え:つる6羽、かめ4匹
鶴と亀以外もある!こんな問題もつるかめ算

つるかめ算は、つるとかめのように異なる足の数を持つ動物の合計と足の数の合計が分かっているときに、それぞれの個体数を求める特殊算です。しかし、問題がかならず「つるとかめ」というわけではありません。他にもこんな問題があります。
つるかめ算数の問題例1
1円玉と5円玉が合わせて28枚あります。その合計金額は76円です。1円玉と5円玉の枚数はそれぞれ何枚ですか?
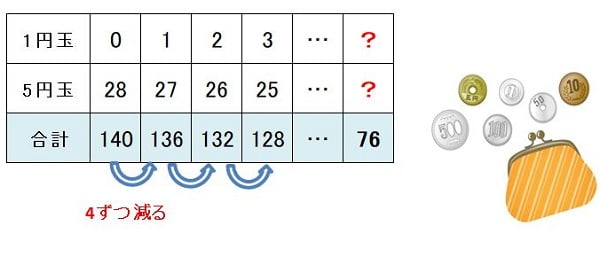
■28枚全部5円だと考えて式を立てると
1.全部5円玉だったとすると総額:5円×28枚=140円
2.本当の金額数との差は:140円-76円=64円
3.1円の枚数は:64円÷(5円-1円)=16枚
4.全部で16枚なので5円の数は:28枚-16枚=12枚
答え:1円16枚、5円12枚
つるかめ算数の問題例2
はじめに分速180m、しばらくして分速170mで歩いたら10分で1780m歩けました。はじめの速度で移動したのは何分ですか?
■10分全部分速180mで歩いたと考えて式を立てると
1.全部180mだったとすると:180m×10分=1800m
2.本当の歩いた距離との差は:1800m-1780m=20m
3.1780m歩いた分数は:20m÷(180m-170m)=2分
4.全部で10分なので180m歩いた分数は、:10分-2分=8分
答え:8分
つるかめ算ができれば中学で習う連立方程式で解ける

今回紹介したつるかめ算の考え方は、じつは中学の連立方程式を使って答えを求めることもできます。
■問:つるとかめが合わせて10匹います。足の数の合計は28本です。鶴と亀はそれぞれ何匹ずついるでしょうか?
1.つるの数をX、かめの数をYとして:X+Y=10
2.足の数は28本なので:2X+4Y=28
3.つるの数は:X=10-Y
4.かめの数につるの数を代入:
2(10-Y)+4Y=28
20-2Y+4Y=28
2Y+4Y=28-20
2Y=8
Y=4
答え:つる6羽、かめ4羽
しかし、小学校ではまだ連立方程式は習いません。XやYなどが分からない子に、連立方程式を教えても頭が混乱するはずです。
それよりも、視覚的に分かりやすく表や図に表して説明したほうが子どもも分かりやすいでしょう。まずは、つるかめ算がどんな計算なのか、どうやって考えるのかを分かりやすく子どもに説明してあげてください。親子で一緒に考えてみるのも良い経験です。
まとめ
つるかめ算は一見難しいと思われがちですが、仕組が分かれば簡単に解くことができます。もちろん、今回紹介したものはつるかめ算の基本でしかありませんが、まずは基本の考え方を理解しましょう。
以前、子どもの宿題に「つるかめ算」出たことがあり、その時は表を使って答えを導き出しました。中学受験では高確率で出題される問題です。もちろん中学受験は考えていなくても、応用問題として親子で取り組んでみるのも良いかもしれません。
表でも、図形でも、子どもが分かりやすい方法で考えてみてくださいね。