植木算の解き方＠基本を抑えれば間違えずにできる

中学受験では様々な問題が出題されます。中でも算数は幅が広く、学校で習わない特殊算も勉強しなければなりません。その中の一つに「植木算」があります。

「植木算」は、道に沿って端から端まで等間隔に木を植えていったとき、必要な木の数を求める計算です。実はこの「植木算」、3年生で習う算数です。そのため「簡単に解ける」と思うかもしれませんが、実は親が思っているほど単純ではありません。

そのため、「できた」と思っていても間違ってしまうのです。そこで今回は、植木算の解き方を紹介します。基本を押さえて、ばっちりにしてみましょう。
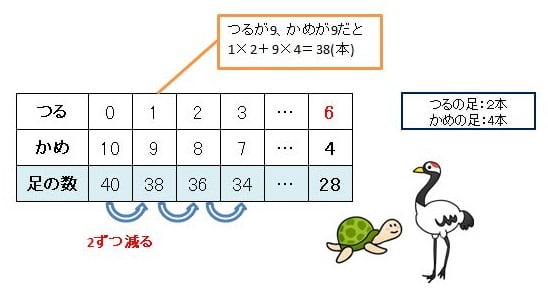
関連記事つるかめ算の解き方がわからない！誰でも簡単にできる基本的な解法

「植木算」の3パターンを制覇すればOK

「植木算」は植えた木の本数を求める問題です。そのパターンは大きく分けて3つあります。

■「植木算」の3パターン

まずは、それぞれのパターンを確認してみましょう。

1．両端に木を植える

【問題】10mの道路に端から端まで2m間隔で木を植えるとき、何本の木が必要でしょうか？

まずは両端にも木を植えるパターンです。間違いやすいのが10mを2mで割って、答えを5本と出してしまうこと。まずは図に書いて確認してみてください。

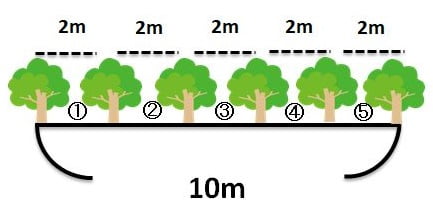
ここで注目するのが木と木の間の数です。10mの道に2m間隔で木を植えると、5つの間ができます。10m÷2m=5本だと、左端に木が植えられていないことになってしまうのです。

そこで、左端にも木を植えることを忘れないようにしましょう。

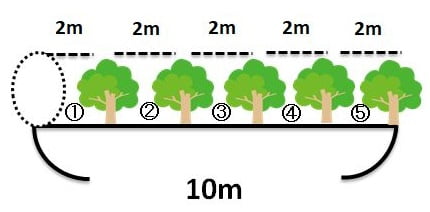
正しくは以下のとなります。

式：(10m÷2m)＋1＝6

答え：6本

2．両端に木を植えない

【問題】バス停から家10ｍあります。この間に2m間隔で木を植えるとすると、木は何本必要でしょうか？

先ほどの問題と違う点は、両端には木を植えないということです。分かりやすくするためにまずは図を描いてみましょう。

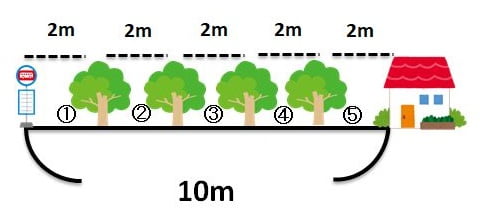
ここでポイントとなるのは、最初と最後には木を植えないということです。

式：(10m÷2m)-1＝4

答え：4本

直線状に木を植える場合、両端を植えるか植えないかで気の本数が変わってきます。問題文をよく読んで、どちらのパターンを問われているのかを考えなければなりません。

3．円形に木を植える

【問題】周囲が30ｍの池の周りに、3ｍ間隔で木を植えました。全部で木は何本必要でしょうか。

今度は円の周りに木を植える問題です。ここでも分かりやすく図に書いてみましょう。

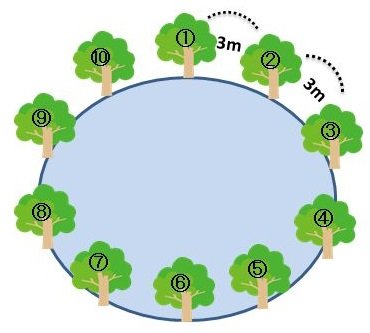
直線の時とは違って、円で考えるときは「木の本数」と「等分する数」が等しくなるので、以下となります。

式：30m÷3m=10

答え：10本

「植木算」の基本は3つです。図に書いて見るとそれほど難しくない「植木算」ですが、問題をよく読んでどのパターンの問題が出題されているのか判断しなければなりません。

ちなみに植木算は、「全体の長さ」に「一定間隔」で物を配置する問題です。『道の植木の間隔』だけでなく『服のボタンの間隔』『紐の結び目の間隔』『勉強時間の休憩の間隔』など問題は様々なパターンが考えられます。

基本が理解出来たら、応用問題にもチャレンジしてみてください。

「植木算」の解き方のコツを覚えよう

「植木算」はコツさえつかめば難しくはありません。そこで、解き方のコツをつかんでおきましょう。

■植木算の公式

■植木算の解き方のコツ

まずは問題が植木算かどうかを見分けることが大切です。分からないときは問題を図に表してみてください。図にすることで、植木算と気が付くこともできます。

さらに公式が思い出せなくても図で理解することもできるのです。特に子どもに教えるときは公式をいきなり伝えるのではなく、図に書いて視覚的に説明をすることで理解が深まります。

まとめ

「植木算」の基本は3パターンです。パッと見ると簡単な計算で答えが求められるものの、間違いやすい特殊算の一つでもあります。

もちろん、「植木算」だからと言って必ず木が出てくるとは限りません。旗や人と人の間隔なども「植木算」です。

さらに木の本数だけでなく、木の本数が分かっていて距離を求める問題もあります。基本をしっかり押させて、いろいろな応用問題にもチャレンジしてみてください。中学受験を検討しているのであれば数をこなすことも大切です。

まずは、基本の問題をばっちり解けるように練習してみてくださいね。