旅人算の解き方をマスターしよう【中学受験の必須問題】

今では中学受験を検討する家庭も多く、中にはクラスの半数が受験をする地域もあるほどです。さらに、受験勉強となると学校で習う学習以外の学習もしなければなりません。

なかでも中学入試の算数は「〇〇算」と名のつくものが数多く出題されます。また学校や塾の宿題で特種算が出ることもあるかもしれません。

そこで今回は特殊算の一つ、「旅人算」の解き方を紹介します。

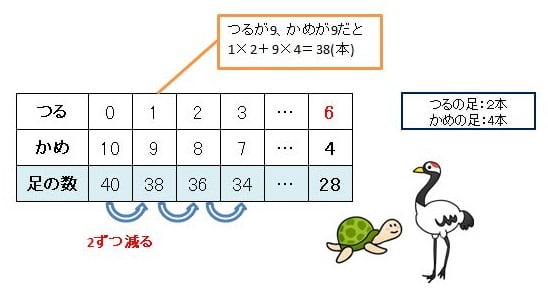
関連記事つるかめ算の解き方がわからない！誰でも簡単にできる基本的な解法

距離や速さを求める旅人算

旅人算とは、旅人(移動する人や物)の速度、移動時間、移動距離などに関する特殊算のことです。

解き方の基本は、「距離＝速度×時間」「速度＝距離÷時間」「時間＝距離÷速度」ですが、中学受験で出題される旅人算は4パターンあります。

旅人算の基本は、2人の距離の差や和、速さの差や和を考えるもの。さらに詳しくは続いて解説します。

4つの旅人算をマスターしよう

旅人算は全部で4パターン。では、それぞれの解き方を確認してみましょう。

1．別の場所から出発して出会う【出会い算】

【問題】図書館と学校間は1km離れています。

Aさんが図書館から学校に向けて分速80ｍで向かい、同じ時刻にBくんは学校から図書館に向けて分速120ｍで向かいました。2人は何分後に出会うでしょうか？

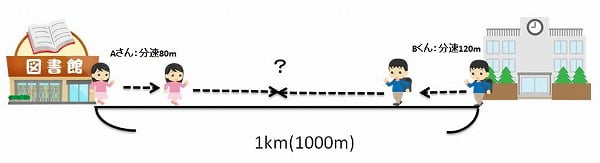
2人が出会うということは、AさんとB君のあいだの距離がゼロになるということです。まずは、1分ごとにどれだけ距離が変わるのかを確認してみましょう。

Aさんは分速120mで進んでいるので、Bくんは分速80mで進んでいるので2人の距離は1分で200m縮まります。

式：1000m÷(120m+80m)=5

答え：5分後に出会う

出会算を公式にすると、次の通り。

上の問題で考えると、二人が出会う時間＝1000m÷(分速120m＋分速80m)となります。

2．同じ道で追いつく【追い越し算】

【問題】1㎞先を毎分30ｍの速さで歩いているAさんを、Bくんが毎分70ｍの速さで追いかけます。BくんがAさんに追いつくのはBくんが出発してから何分後でしょうか。

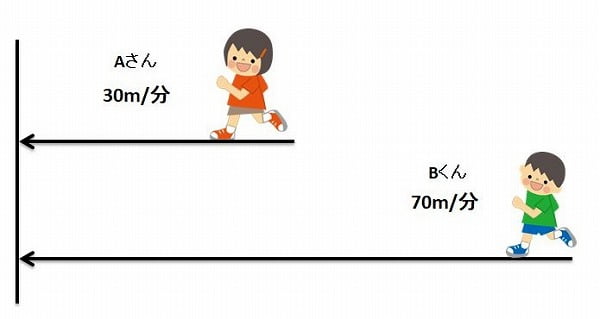
まず、1分でどれだけ距離が縮まるかを考えてみてください。Aさんは30m、Bくんが70mで歩くと1分間に、70－30＝40(ｍ)ずつ近づいていくことがわかります。1km(1000m)の距離が毎分40m縮まると

1000m÷(70m－30m)=25分

答え：25分後に出会う

という計算をすることができるのです。

3．同一円周上で同じ向きに進む

【問題】A君とB君は、1周3200mの池の周りをランニングしています。今2人が同時に同じ向きに走り出します。A君の走る速さは毎分200m、B君の走る速さは毎分120mです。A君は何分後にB君を追い抜くでしょうか。

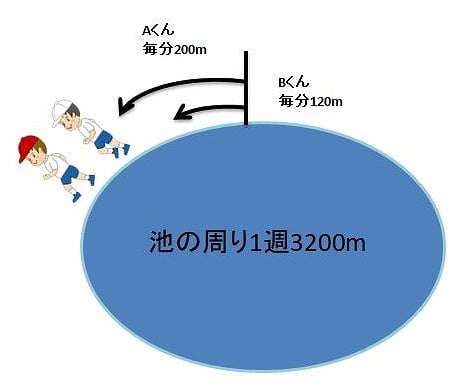
ポイントは、同時にスタートして追い越すまでには3200m距離を縮めなければなりません。AくんとB君が同時に走り出して1分後には80mの距離が縮まります。

式：3200m÷(120m－40m)＝40(分)

答え：40分後に追い越す

4．同一円周上で反対向きに進む

【問題】AさんとB君は、1周4500mの池の周りをサイクリングしています。今2人が同時に反対向きにこぎ始めました。Aさんの速さを毎分400m、B君の速さを毎分500mとするとき、2人が出会うのは何分後ですか。

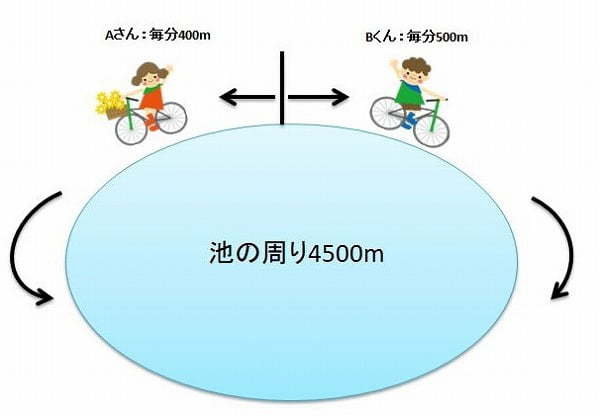
お互い反対向きに進むので、1分あたり400m＋500m＝900m近づくことになります。2人の距離の差は池の1周分4500mになるので、この差を何分でなくすことができるかを考えてみましょう。

式：4500m÷(400m＋500m)=5

答え：5分後

上記で紹介した4つのパターンが旅人算の基本的な考え方になります。基本的な距離の求め方を知っていれば、簡単に解くことができるのです。

他にもまだまだある旅人算の問題

旅人算の基本は6年生で習う速さの単元の応用です。基本が分かればそれほど難しくはないものの、中学受験などでは基本ではなく少しひねった応用問題が出題されます。

そこで、もう少しレベルアップした問題にチャレンジしてみましょう。

1．折り返しの問題

【問題】マラソン大会のコースは6kmで、中間の3kmの地点で折り返して戻ってくるコースです。A君は分速300m、B君は分速200mで走ります。A君が折り返してB君とすれ違うのはスタートしてから何分後でしょう。

(写真：190703_旅人算の解き方をマスターしよう【中学受験の必須問題】【05】)
まずは、折り返しの3kmの地点にA君が付いた時間と、その時のB君の位置を求めてみましょう。

A君が折り返し地点までかかった時間

式：3000m÷300m=10分

スタートから10分後にはA君は折り返し地点にいます。B君の10分後は次の通り。

式：10分×200m＝2000m

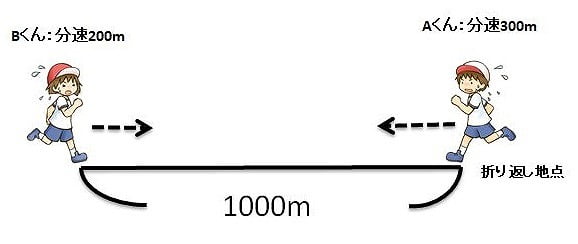
つまり、スタートして10分後にはA君は折り返し地点に、B君はあと1000mで折り返し地点という場所にいます。ここからお互い1000m向かい合って走ることになるので、出会い算を思い出してください。

A君は300m、B君は200m進むので1分間に500mの距離が縮まります。2人が出会うまでの時間は次の通り。

式：1000m÷500m=2分

すでに10分経っているので式と答えは以下のとなります。

式：10分＋2分＝12分

答え：12分後

距離を求める応用問題

【問題】Aさんは分速60mの速さで学校から公園へ歩いて向かいます。Aさんが家を出てから10分後にBさんが分速180mの速さで学校から公園へ走って向かうと、2人は同時に公園に到着しました。学校から公園までは何mでしょう。

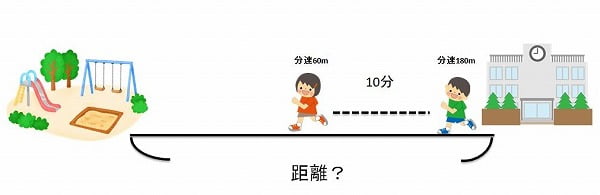
2人は同じ方向に進んでいます。B君が学校を出るまでにAさんはすでに10分歩いています。

10分後のAさんが歩いた道のりは次の通り。

分速60m×10分＝600m

B君が学校を出る時点で2人は600m離れていることがわかりました。1分間に縮まるふたりの距離は、180m－60m＝120mです。よって、B君がAさんに追いつくまでにかかる時間は、

600m÷120m＝5

答え：5分

B君がAさんに追いつくと同時に公園に到着するので、B君は学校から公園まで5分かかったということになります。その間に走った道のりは次の通り。

式：分速180m×5分＝900m

答え：900m

まとめ

今回紹介した問題以外にも、3人で同時で出発した場合や、時間を求める問題なども出題されるかもしれません。まずは、基本の4パターンをしっかりと理解してみてください。

基本は距離の公式が分かっていれば簡単に求めることができます。後は、いろいろなパターンの問題を解いて慣れることが大切です。